KMP算法

KMP算法我曾今写过一篇博客讲过，但是我当时觉得这个算法好烂，就没细讲，后来发现他们还挺喜欢考这个算法的，于是我再开帖讲一下

自然语言描述

自然语言描述是我根据《algorithm》的内容以及我自己的理解写出来的，，一般来说是正确的计算next[]与解释KMP的算法，这个方法比较考验悟性，但是原理确实是这样😂

考研教材解释

我们还是拿pat=abcac举例子，我们从a开始取字串，然后找前缀与后缀的最长相等长度

• ”a“最长相等长度为0

• “ab”最长相等长度0

• “abc”最长相等长度0

• “abca”最长相等长度1

• “abcac”最长相等长度0

所以我们可以得到PM={0,0,0,1,0}

但是我们有公式右移位数=已匹配的字符数-对应的部分匹配值

然后 对应的部分匹配值 是 j 前一个值，于是为了方便我们把PM整体右移一位，并用-1作为next[0]的值，得到next[]={-1,0,0,0,1}

所以我们有公式：

Move=(j-1)-next[j]

这就相当于我们将J回退到：

j回退到的位置=j-Move=j-((j-1)-next[j])=next[j]+1

所以我们就可以都得到next[]的新的形式：

next[]={0,1,1,1,2}

这里next[]的含义是在j处匹配失败后，j回退到的位置

拓展：更底层的匹配方法

实际上，KMP算法应该生成一个有限状态自动机（DFA），然后通过DFA去匹配字串

继续按照pat=abcac为例，画出的DFA如下：

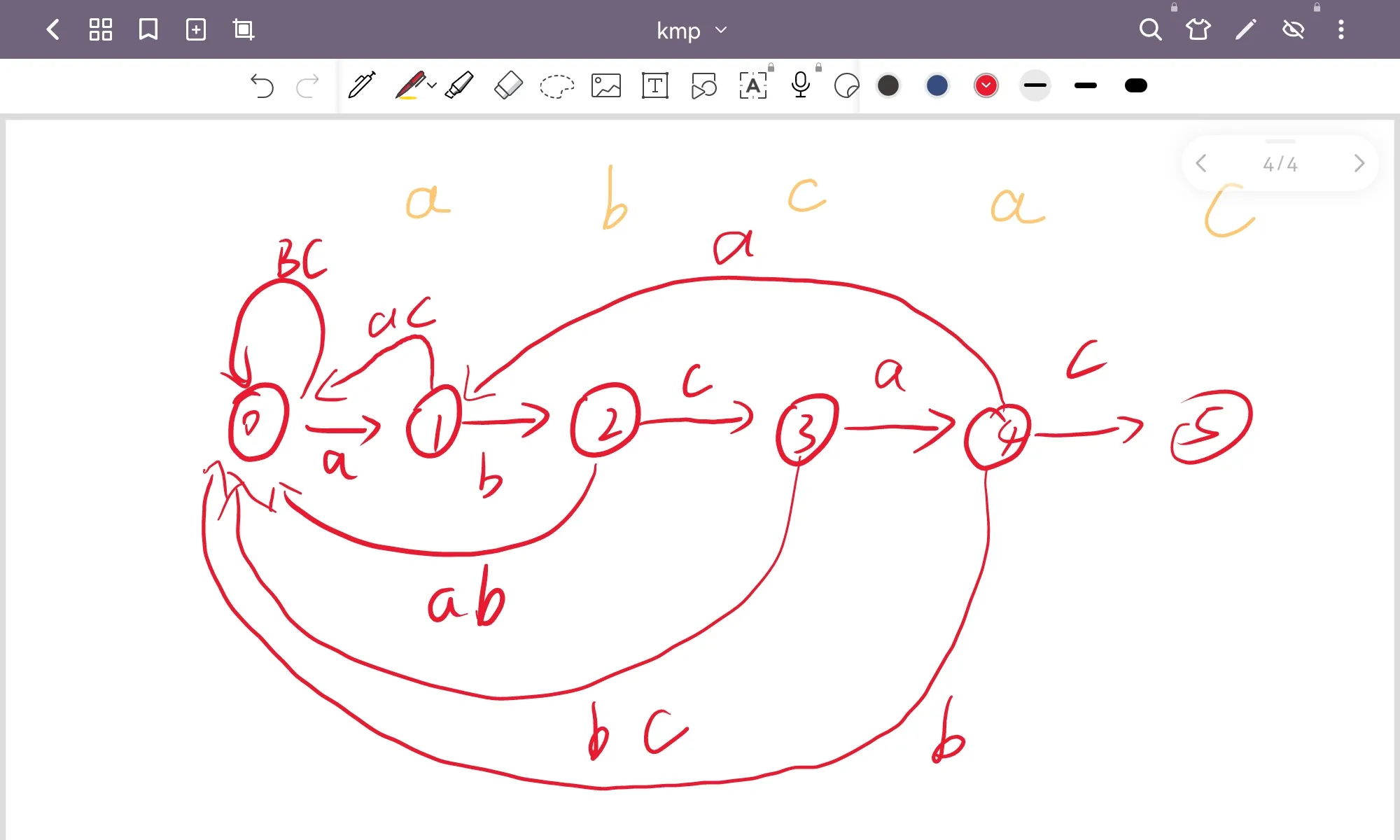
生成DFA的算法如下

/*KMP字符串查找*/
class KMP
{
private:
	std::string pat;
	const static int r = 256;
	int *dfa[r];    //建立一个二维数组
public:
	KMP(std::string pat)
	{
		this->pat = pat;
		int m = pat.length();
		for (int i = 0; i < r; i++)
		{
			dfa[i] = new int[m];
			std::fill(dfa[i], dfa[i] + m, 0);
		}
		dfa[pat[0]][0] = 1;
		for (int x = 0, j = 1; j < m; j++)
		{
			for (int c = 0; c < r; c++)
			{
				dfa[c][j] = dfa[c][x];	//复制匹配失败情况下的值
			}
			dfa[pat[j]][j] = j + 1;		//设置匹配成功情况下的值
			x = dfa[pat[j]][x];		//更新重启状态
		}
	}
	int seatch(std::string txt)
	{
		int i, j, n = txt.length(), m = pat.length();
		for (i = 0, j = 0; i < n&&j < m; i++)
		{
			j = dfa[txt[i]][j];
		}
		if (j == m)
			return i - m;		//找到匹配
		else
			return n;		//未找到匹配
	}
};